由正方体引起的探索规律题

-------第五周反思

第1316期第一周数学报有一题是这样的： 第一幅图是1个正方体，第二幅图是2个正方体上下叠在一起，第三幅图是3个正方体上下叠在一起。。。。。。。。探索第n幅图小正方体个数与露在外面的面数的变化规律。

我引导同学们思考，变和不变的分别是哪些面？学生很快就发现，最上面的那个面不变，一直存在，而每增加一个正方体，就增加4个面，发现第n幅图小正方体个数与露在外面的面数的变化规律是4n+1。

学生掌握这题之后，我又在黑板上出示了几幅图：

每边用一根火柴棒， 一直这样摆下去，摆n个正方形需要多少根火柴棒？

     由于有了上一题的引导，学生很快知道从不变和变化两个方向观察图形，得出结论3n+1。

     于是我又问，同学们你们能做小老师，出一些题目给老师做吗？学生非常踊跃，有的这样出题：

每边用一根火柴棒， 一直这样摆下去，摆n个等边三角形需要多少根火柴棒？

有的这样出题：

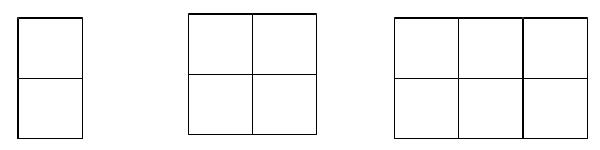
每边用一根火柴棒， 一直这样摆下去，摆n个“日”字形需要多少根火柴棒？

学生觉得自己做了一回小老师，对这种规律题的理解更透彻了一些，对数学的学习积极性也更提高了一些。