第五周：学生教会了我第二种解题妙方

江苏省常州市新北区新华实验小学 姚建法

为了适当激发学生兴趣、提升数学思维能力，我在课后留了一道思考题，并扬言：这里有道“超级思维题”，看看谁能做出来。做出来的同不将会得到意想不到的礼物！

“大正方形面积是10平方分米，小正方形面积是8平方分米，阴影部分面积是多少平方分米？” 

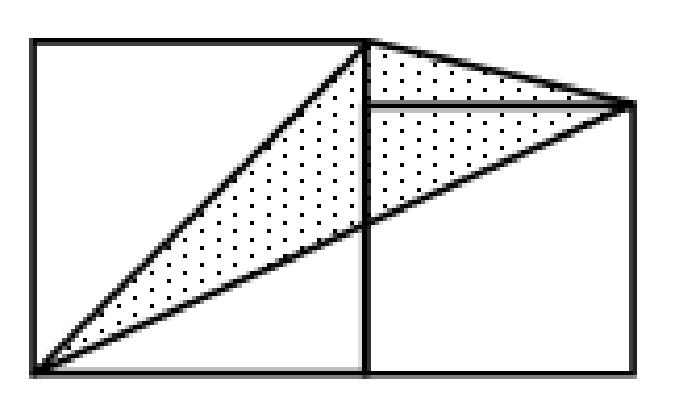
当即便有学生说“这不就是练习册上的么？”，我一听，心想：“真好,能知道联系思考了”,数学学习本身也是一种“求联”的学问。

于是我说：“真一样吗？如果一样，还会是‘超级思维题’吗？好好比一比什么地方变了。”

练习册上是已知了大、小正方形的边长，便能分别求出空白部分面积，并且没右上角的连线而成的小三角形。而此题更在于无法通过边长求分别求出分割而出的所有小图形的面积，这也正是学生最大的思维挑战所在。

怎么办？自由学生思考一夜。

第二天交流时，学生无人能作答。

我便问问：“既然没有办法解决，那你们先猜猜看，觉得面积可能是多少？”

数学猜想，作为一种数学直觉，这也是对数感的一种把握的尝试与经历。

学生便有了（10+8）的一半、8、10的一半等等之类的猜想。

那么到底对不对呢？学生希望我讲解一下。我在黑板上依次画了如下图组让学生去比较、去体会、去思考：

慢慢地，有学生有反应了，逐渐地，情绪显得激动起来。

“右边的正方形越变越小，阴影面积慢慢变成了左边正方形面积的一半，所以它的面积是10的一半，也就是正确答案应该是5。”

其实，在这种思维方式里，展现的是一种极限思维。我没有明说。

受此“一半”的启发，数学课代表贾力昂兴奋了起来：老师，我觉得还可以这样思考（上黑板讲解）：把1号三角形旋转到2号空白处，它们面积相等。

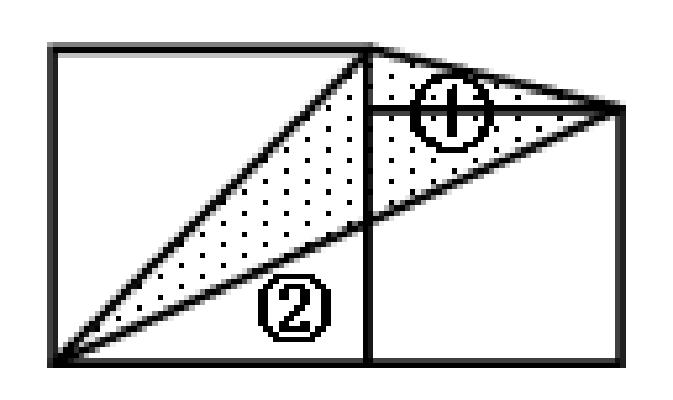
“那你如何证明它们面积相等呢？形状又不一样。”面对疑问，贾同学答不上来了。

“如果是第一幅图该多好，一看就是相等的。”我来打圆场。学生们表示赞同。看着贾力昂黑板上的草图，突然，我想到解决1号与2号三角形面积相等的办法。“贾力昂的思路其实还是管用的，如果把这里一连，再把这些擦去，那么就---”（从正方形与对角线，得出两个等腰直角三角形，对角线是互相平行的，便构造出了一个梯形。）

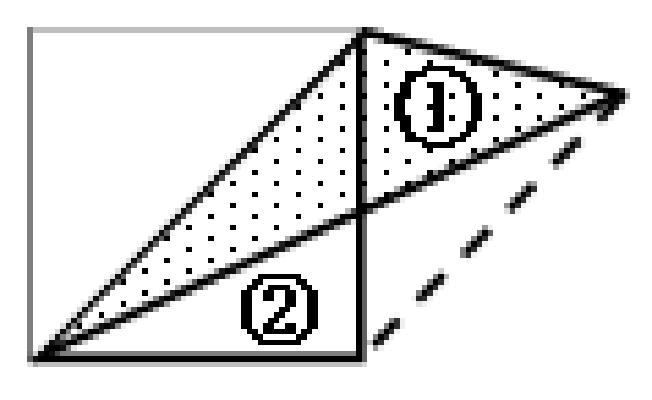
“练习册上也有，昨天我们刚做的！那两个三角形面积相等的。”于是，练习册上的另一题再次进入学生的视线。

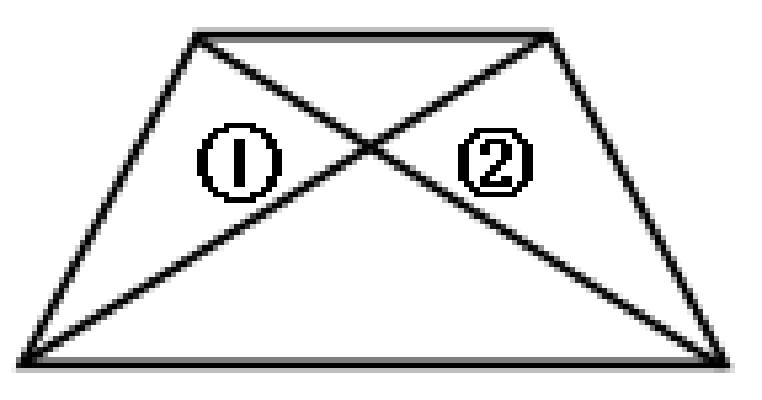
数学是求联的，它不仅仅研究数与形，更是需要研究数之间的关系，以及形之间的关系。

今天，我从贾力昂同学的“直觉”缺陷中，获得启示，我们师生一起将三个“图形问题”进行了有效链接，产生联系，形成了奇妙的效应，一起经历了一次奇妙的数学之旅，提升了数学思维能力，更重要的是增强了对数学的兴趣。

20161004