第一周：板书上的形符与数学化

新北区新华实验小学  姚建法

开学第一课，上的是五年级下册“方程的意义”，其核心本质不是认识方程或等式，而是体会左边与右边的“相等”关系。

今天的板书，是灵机一动的，为了更好地体会抽象的“相等”，逐步形成了如下的并不工整的板书，尝试用形符的方式体现数学化的过程。

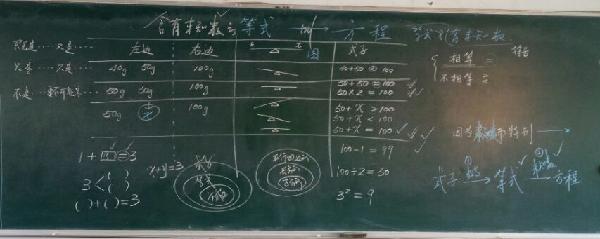
    一、抓住相等本质，用“左边”“右边”进行体会与强化。

    曾经这节课更多的老师（包括我）更多地站在“等式”与“方程”的外在形态上，也用天平或翘翘板进行形符式的“图式”化数学过程，明确单拎的左与右的体验并不强烈。立足所教班级基础弱的特点，通过板书与对学生分开书写的引导，更好地对等式的“等”进行慢体会。

二、借用直观图式，用“示意图”逐步表达三类数量关系。

学生对于生活中的天平与翘翘板是有深刻体会的，能够较好地理解，如何从中与数学进行较好的抽象与勾联，画示意图是种方法，形象而直观，对后进生多的班级应该更加适用些。

观察了左边与右边，表达了直观形符图，学生再得出“式子”后的分类就显得深刻了，不再是停留在表面的关系符号上，而是能用等式的核心本质“左边=右边”来数学化天平两边的关系。

三、用学生的语言来组织等式与方程的概念。

有了生活情境再现、形符式符号化过程、式子的抽象分类，学生再来表达什么是等式，并从等式中分离出方程来也就不再那么困难。学生用自己的体会与语言来表达什么叫方程，陶彥凝说得好：一是要左边和右边相等，二是要有未知数。石娜娜说：要左边和右边相等的有未知数的式子，都一一道出了方程的本质内涵。于是通过适当调整得出方程的课本式表达“含有未知数的等式叫做方程”。

四、抓住知识的前后联系，让知识之间建立必要的关联

再怎么看起来孤立的知识也总有或多或少、或紧或松的关联。一方面等式与方程的包含关系图（集合图）可以与四边形（长方形正方形）、三角形（按边分类）等类比，这样集合图就不再那么陌生而高深。另一方面与一、二年级时的括号、方框等反刍，使得更容易明白只要是未知数，字母、方框等只是未知数的表达外显不同而已，本质却是相同的。第三方面在判定等式与方程时可以与语文表达中的关联词融合，较好地把握住了等式与方程的递进性与特殊化，更好地体会数学表达的严谨性与简洁性，学生表达起来也比较地方便：XX即是等式，又是方程（不但……而且）；XX只是等式，不是方程；XX不是等式，更不可能是方程。

知识求联，概念的本质内核通过形符化的手段可以尽可能地物化与外显，通过直观，更好地面向优秀生以表达的方式强化，给予后进生们更好地降低理解的难度，从而形象地逐步跟上其他学生前进的步伐。