这几天在复习第一单元和第二单元的内容，第一单元在方格纸上把简单图形按顺时针或逆时方向旋转90°是教学的难点。由于年龄特征限制、空间观念的影响，在类似于把梯形①绕A点顺时针旋转90°的习题中，学生的错误屡见不鲜：

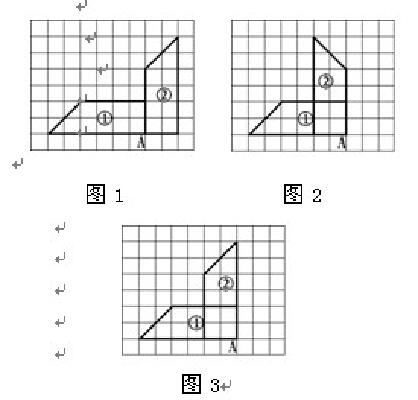
图形旋转有三个关键要素：一是旋转的中心，即绕哪一个点旋转；二是旋转的方向；三是旋转的角度。我从学生的作业中搜集了3种典型错例：图1旋转的中心点、方向和角度都没有问题，但旋转时把梯形的上底和下底搞混淆，导致梯形“斜腰”的方向明显出现了错误。图2乍一看挺像，仔细观察会发现梯形没有绕着A点进行旋转，旋转的中心点发生了错误。图3“叠加”了图1和图2的错误，旋转中心点以及梯形的上底和下底在旋转时都出现了偏差。

【错因分析】

原因一：学生思维形象性与问题抽象性之间的冲突。在小学阶段，学生思维的特征主要是从具体形象思维向抽象逻辑思维过渡发展的。到了中高年级，学生的抽象思维仍然带有很大的具体形象性，仍然需要感性材料的支持。在方格纸上旋转梯形，要远比教材中所列举的收费站道口的转杆打开和关闭的实物旋转来得抽象。纵观“图形旋转”单元的教学，如果仅从转杆的打开和关闭，直观形象地来理解顺时针、逆时针方向以及旋转的中心点。在此基础上直接抽象过渡到在方格纸上画出平面图形旋转后的图形，两者之间的思维跨度太大。对于四年级学生而言，没有任何实物作为参照，一下子就要在脑海中描绘出梯形旋转后的样子并画出来，难度不可谓不高。由于学生思维形象性与问题的抽象性之间的冲突，出现旋转中心点的偏差以及梯形上底和下底“张冠李戴”的现象，也就不足为奇了。

原因二：空间观念的培养与教学设计之间的脱节。空间观念的培养是长期经验积累的过程。教学中我们发现，即便学生借助简易梯形进行旋转，在头脑中内化成合理的表象，弥补了思维形象性和问题抽象性之间的冲突，但因为缺少具体、细致的方法支撑，学生仅凭着对图形的感觉，在方格纸上画出旋转后的梯形，错误也在所难免。“粗口径”“大梯度”的教学设计，脱离了学生空间观念的实际，使得学生的学习浮于表面、没有根植地气，也就不利于学生获得成功的体验。因此，在方格纸上如何画出旋转后的图形？有哪些方法和技巧？这需要教者进行思考，并针对教材进行必要、适度补充，避免学生空间观念与教学设计之间形成脱节。

原因三：解答问题与自我反思习惯之间的分离。反思是数学思维活动的核心和动力，作业中的“回头看”就是学生进行的自我反思。旋转梯形时需要学生进行“回头看”：可以顺向检查，即将题目逐步再做一遍；也可逆向比对，即将旋转后的图形反方向旋转与问题进行比较。在“正”与“逆”的反思中帮助学生养成自我反思的习惯，从而获得数学的理解。学生之所以出现在梯形旋转时“不知所云”“漏洞百出”，而订正时却又能“恍然大悟”“后悔不迭”。究其原因，主要是把“解决问题”等同于“解答习题”，认为仅仅运用已有的知识按一定的程序得出题目的答案即可，忽略了寻求解决方法的过程，忽略了策略的优化、提炼，没有真正意义上的回顾与反思、检查与完善。

【改进措施】

措施一：思维从直观操作走向表象内化。为了有效解决学生思维形象性与问题抽象性之间的冲突，不妨引导学生用纸片做个简易的梯形，旋转操作，看看旋转后的图形究竟是什么样子。在动手操作的过程中学生的内部语言也就随之悄悄展开，在操作中获得的形象和表象，及时推动着他们进行分析、综合、比较、概括，引起和促进学生把外显的动作过程和内隐的思维活动紧密结合起来。一旦表象内化，学生就会自然地在头脑中构画草图，把握梯形旋转的大致形状，也就不会出现诸如图1和图3将上底和下底混淆，导致梯形“斜腰”明显改变了方向的错误。当然从具体的直观操作到脱离实物直接想象，是一个渐变的过程，需要老师的引导和学生自觉的内化。

措施二：方法从整体思考走向局部分解。有研究表明，一维、二维与三维图形的相互转换是培养学生空间观念的主要途径。 “点”和“线”是学生空间观念形成的基础。因此，把平面图形的旋转进行有效分解，从一维空间入手，抓住“点”“线”的位置变换，化难为易，知难而“退”，可以有效弥补学生现有实际空间观念和教材要求之间的脱节，便于解决问题，也就不会出现类似于图2和图3的错误。梯形旋转中，关键的“点”是旋转的中心点A，关键的“线”是梯形的上下两条底边。教者要引导学生找准关键“点”，思考关键“线”。讨论梯形的上底和下底，旋转后应分别在方格纸的哪条边上，旋转后各应画几格的长度。确定好关键“线”旋转后的位置及长度，又有直观操作和表象内化作为基础，旋转梯形的错误一定会大大减少。

措施三：习惯从教师引导走向学生自觉。学生反思习惯的培养要经历三重境界：第一重境界是对题目的反思，如：旋转梯形时，A点的位置会发生变化吗？梯形的两条底边旋转后应分别在哪两条边上？直角梯形另一条斜着的腰旋转后应是什么样子？第二重境界是对解题方法的反思，如：怎样抓住关键的“点”“线”来确来旋转后图形的位置？第三重境界是对解题策略和数学思想的反思，如：旋转梯形时借用直观操作将抽象问题形象化，抓住关键“点” “线”将复杂问题简单化，这些是方法和策略你在哪儿也遇到过？对你解决数学问题有什么启示？多层次的反思活动为学生的可持续发展提供可能。