在教学“三角形的分类”这部分内容时，我首先出示6个三角形，让学生根据每个三角形角的大小填表，然后观察表格，把三角形分成锐角三角形、直角三角形和钝角三角形三类。之后，我介绍说：把所有三角形看做一个整体，用一个椭圆表示，锐角三角形、直角三角形、钝角三角形是这个整体的一部分，可以这样表示：

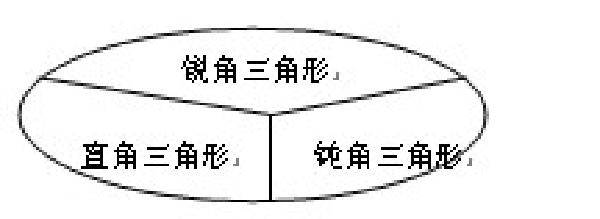
这时一个学生站起来说：“老师，这里用椭圆不好。”我看了看屏幕，一脸疑惑地问道：“怎么不好？”“因为它们三个面积不一样，使人感觉它们的个数有的多，有的少。但是它们的个数不能说谁多谁少。如果用圆表示，可以平均分成三份，每份一样多。”一石激起千层浪，原本安静的课堂立即热闹起来……

   为什么我们看来无可置疑的集合图，在学生那里却有这样的想法？四年级的学生，其思维水平正处于具体运算阶段，以形象思维为主，虽然以直观图来表征数学概念、关系是符合其思维发展实际水平的，但是有时学生对图形究竟表征的是什么会有困惑。例如，在学习分数中，把一个图形平均分成3份，每份是形状相同、面积大小一样的三块，学生容易得出每份是这个图形的1/3。

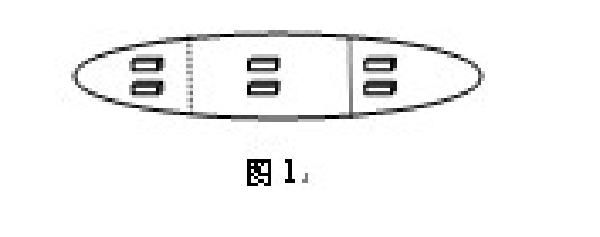
而对像图1这样的问题，有的学生会从图形上看不是1/3，需要教师提醒要看的是长方体的个数。学生对图形各部分面积并不相等的感知干扰了问题的本义。

后来，我让学生自己想办法表示分类的结果，让学生有充足的时间思考，真实地表达心中的想法。我们不妨看看学生的作品：

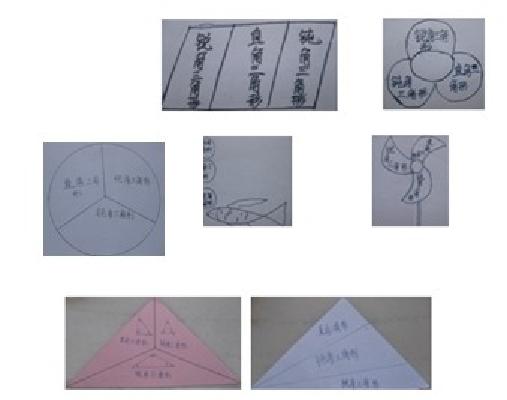
实际上，学生普遍的想法是，尽管图形的形状可以灵活多变，但要用完全相同的图形来表示可以分成的三个部分。教师需要肯定和鼓励学生的创造，也可以相机提醒学生如果用椭圆来表示，这里的椭圆只是表示“所有的三角形”，每一部分表示的是不同种类的三角形，具体大小与表示三角形的数量无关，不需要严格地把椭圆评价分成三份。

总之，学生看似不合理的想法，往往都会暴露其真实的思维过程，值得我们慎思。