第十五周：适当向后拓一拓：因为需要，所以有效

小学二年级数学还蛮好玩的。

二年级数学89页有这样一道思考题：

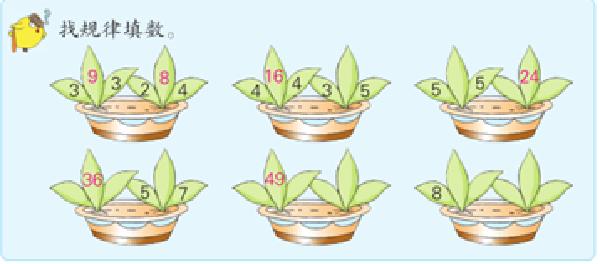
学生通过自己的观察与计算，个别同学加上适当的合作交流，是能够找出规律、并正确填对的，主要是在“24”时纠结了一下：因为有两个乘法口诀“三八二十四、四六二十四”。只是他们一时难以用数学语言来表达，能够分别用类似于“1号叶子与3号叶子相同，1号叶子比4号叶子大1，3号叶子比6号叶子小1，2号叶子是1号与3号的乘积，比5号叶子大1，5号叶子是4号与6号叶子的乘积”进行解释。学生具备了一定的把几个数据进行关联思考的能力。事实上，这就是中学所学的平方差公式中的基本型：（a+1）×(a-1)= a×a – 1。只是学生想不到，也不可能想到，并且还不适宜想到（五年级下册才具体学习用字母表示数）。

如何让这个规律更加“有用”呢？个人以为最大的方法是让学生有需求：因为需要，所以这个规律有效。于是我展开了拓展：用图形进行表征，边说边在黑板上进行板书：

学生群可热闹了！因为没有学过这么大的“乘法口诀”，当★×★=121一写完就懵了。当○×□=？出来时也还没底，但当箭头与-1、+1出来后，沸腾了！一开始有学生喊121，一晃，就是大面积的120了。相信通过这个环节的适时拓展，学生的感受是丰富且深刻的，对于长期发展是有效的。

我没有再追问是怎么想的，只是说了一句：掌握了一定的规律与方法，就算没学过的问题，也有办法解决。

有时的拓展，需要清晰地掌握；而更有时候的拓展，只需蜻蜓点水、适时渗透即可。

另：对教材的一点建议是：如果把中间的2号与5号叶子改成花朵，甚至可以红花、黄花，那么是否更利于学生展开规律的言语表达：两边叶子相乘的积是中间的花，红花比黄花……